7.3 Objective functions, metrics, and evaluation

1. Convergence.
   1. [E] When we say an algorithm converges, what does convergence mean?
   2. [E] How do we know when a model has converged?
2. [E] Draw the loss curves for overfitting and underfitting.
3. Bias-variance trade-off
   1. [E] What’s the bias-variance trade-off?
   2. [M] How’s this tradeoff related to overfitting and underfitting?
   3. [M] How do you know that your model is high variance, low bias? What would you do in this case?
   4. [M] How do you know that your model is low variance, high bias? What would you do in this case?
4. Cross-validation.
   1. [E] Explain different methods for cross-validation.
   2. [M] Why don’t we see more cross-validation in deep learning?

5. Train, valid, test splits.

   1. [E] What’s wrong with training and testing a model on the same data?
   2. [E] Why do we need a validation set on top of a train set and a test set?
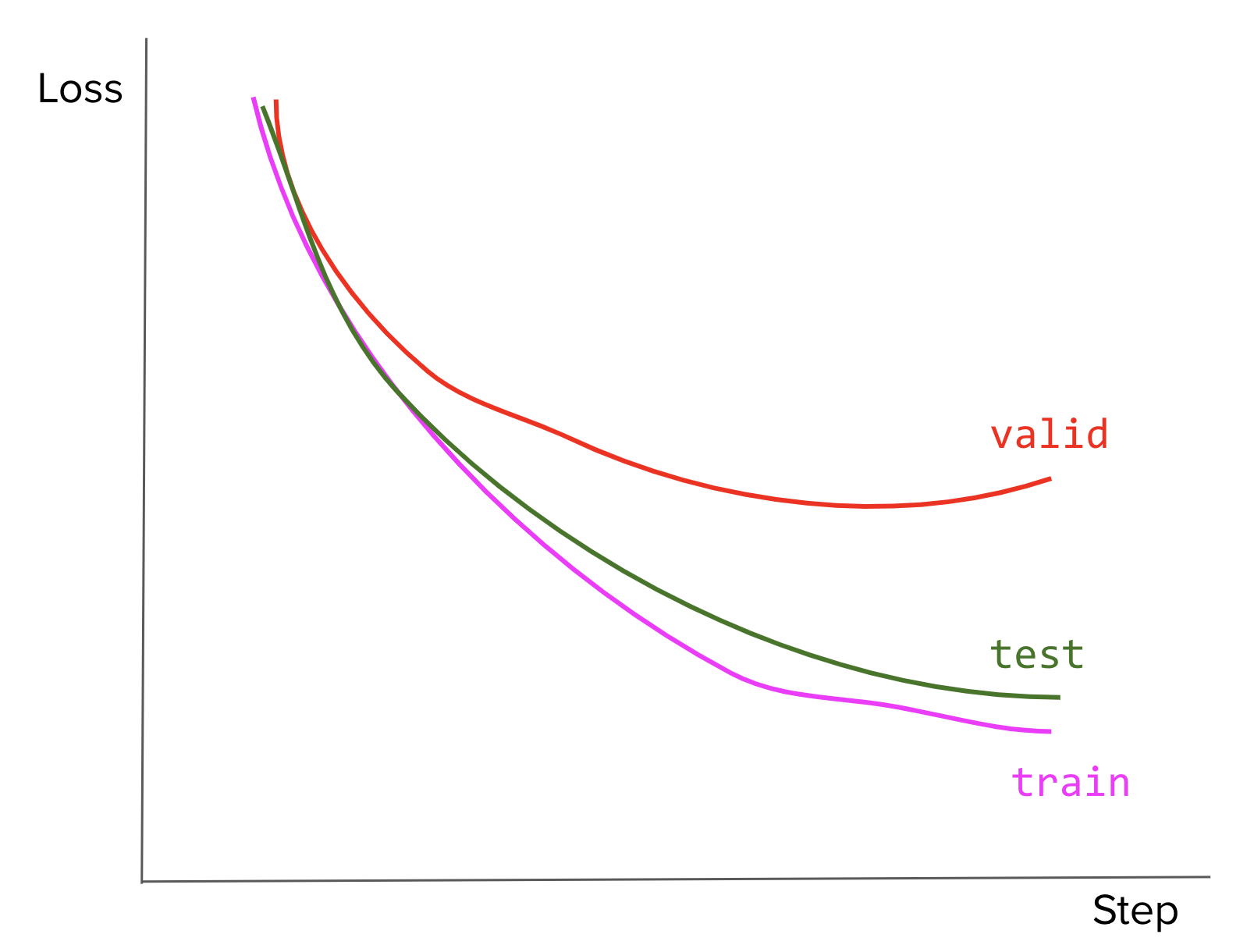
   3. [M] Your model’s loss curves on the train, valid, and test sets look like this. What might have been the cause of this? What would you do?
   

6. [E] Your team is building a system to aid doctors in predicting whether a patient has cancer or not from their X-ray scan. Your colleague announces that the problem is solved now that they’ve built a system that can predict with 99.99% accuracy. How would you respond to that claim?

7. F1 score.
   1. [E] What’s the benefit of F1 over the accuracy?
   2. [M] Can we still use F1 for a problem with more than two classes. How?

8. Given a binary classifier that outputs the following confusion matrix.

   	Predicted True	Predicted False
   Actual True	30	20
   Actual False	5	40

   1. [E] Calculate the model’s precision, recall, and F1.
   2. [M] What can we do to improve the model’s performance?
9. Consider a classification where 99% of data belongs to class A and 1% of data belongs to class B.
   1. [M] If your model predicts A 100% of the time, what would the F1 score be? Hint: The F1 score when A is mapped to 0 and B to 1 is different from the F1 score when A is mapped to 1 and B to 0.
   2. [M] If we have a model that predicts A and B at a random (uniformly), what would the expected F1 be?
10. [M] For logistic regression, why is log loss recommended over MSE (mean squared error)?
11. [M] When should we use RMSE (Root Mean Squared Error) over MAE (Mean Absolute Error) and vice versa?
12. [M] Show that the negative log-likelihood and cross-entropy are the same for binary classification tasks.
13. [M] For classification tasks with more than two labels (e.g. MNIST with 10 labels), why is cross-entropy a better loss function than MSE?
14. [E] Consider a language with an alphabet of 27 characters. What would be the maximal entropy of this language?
15. [E] A lot of machine learning models aim to approximate probability distributions. Let’s say P is the distribution of the data and Q is the distribution learned by our model. How do measure how close Q is to P?
16. MPE (Most Probable Explanation) vs. MAP (Maximum A Posteriori)
    1. [E] How do MPE and MAP differ?
    2. [H] Give an example of when they would produce different results.

17. [E] Suppose you want to build a model to predict the price of a stock in the next 8 hours and that the predicted price should never be off more than 10% from the actual price. Which metric would you use?

    Hint: check out MAPE.

In case you need a refresh on information entropy, here's an explanation without any math.

Your parents are finally letting you adopt a pet! They spend the entire weekend taking you to various pet shelters to find a pet.

The first shelter has only dogs. Your mom covers your eyes when your dad picks out an animal for you. You don't need to open your eyes to know that this animal is a dog. It isn't hard to guess.

The second shelter has both dogs and cats. Again your mom covers your eyes and your dad picks out an email. This time, you have to think harder to guess which animal is that. You make a guess that it's a dog, and your dad says no. So you guess it's a cat and you're right. It takes you two guesses to know for sure what animal it is.

The next shelter is the biggest one of them all. They have so many different kinds of animals: dogs, cats, hamsters, fish, parrots, cute little pigs, bunnies, ferrets, hedgehogs, chickens, even the exotic bearded dragons! There must be close to a hundred different types of pets. Now it's really hard for you to guess which one your dad brings you. It takes you a dozen guesses to guess the right animal.

Entropy is a measure of the "spread out" in diversity. The more spread out the diversity, the header it is to guess an item correctly. The first shelter has very low entropy. The second shelter has a little bit higher entropy. The third shelter has the highest entropy.