Key trends from NeurIPS 2019
With 51 workshops, 1428 accepted papers, and 13k attendees, saying that NeurIPS is overwhelming is an understatement. I did my best to summarize the key trends I got from the conference. This post is generously edited by the wonderful Andrey Kurenkov.
Disclaimer: This post doesn’t reflect the view of any of the organizations I’m associated with. NeurIPS is huge with a lot to take in, so I might get something wrong. Feedback is welcome!
Table of Contents
- Deconstructing the deep learning black box
- New approaches to deep learning
2.1 Deep learning with Bayesian principles
2.2 Graph neural networks
2.3 Convex optimization - Neuroscience x Machine Learning
- Keyword analysis
- NeurIPS by numbers
- Conclusion
1. Deconstructing the deep learning black box
Lately, there has been a lot of reflection on the limitations of deep learning. A few examples:
- Facebook’s director of AI is worried about the computational wall. Companies should not expect to keep making progress just with bigger deep learning systems because “right now, an experiment might be in seven figures, but it’s not going to go to nine or ten figures .. nobody can afford that.”
- Yoshua Bengio gave Gary Marcus as an example of someone who frequently points out deep learning’s limitations. Bengio summarized Gary Marcus’s view as “Look, deep learning doesn’t work.” Gary Marcus disputed this characterization.
- Yann Lecun addressed this trend: “I don’t get why, all of a sudden, we read all these stories and tweets that claim ‘progress in AI is slowing’ and ‘Deep Learning is hitting a wall’ … I have been pointing out those two limitations and challenges in pretty much every single one of my talks of the last 5 years … So, no, the identification of these limitations is not new. And there is no slow down.”
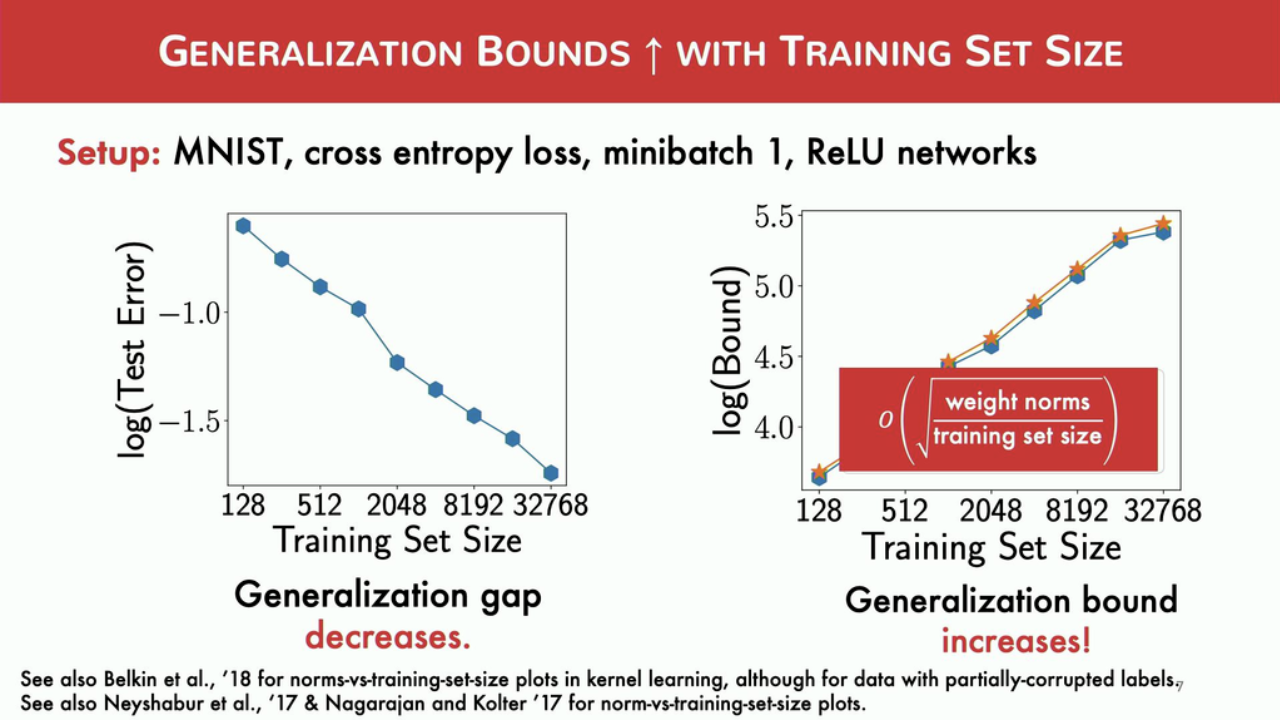
In this climate, it’s nice to see an explosion of papers exploring the theory behind deep learning, why and how it works. At this year’s NeurIPS, there are 31 papers on the convergence of various techniques. The outstanding new directions paper award goes to Vaishnavh Nagarajan and J. Zico Kolter’s Uniform convergence may be unable to explain generalization in deep learning, with the thesis that the uniform convergence theory by itself can’t explain the ability of deep learning to generalize. As the dataset size increases, theoretical bounds on generalization gap (the gap between a model’s performance on seen and unseen data) also increase while the empirical generalization gap decreases.
The neural tangent kernel (NTK) is a recent research direction which aims to understand the optimization and generalization of neural networks. It came up in several spotlight talks and many conversations I had with people at NeuIPS. By building on the well-known notion that fully connected neural nets are equivalent to Gaussian processes in the infinite-width limit, Arthur Jacot et al. were able to study their training dynamics in function space instead of parameter space. They proved that “during gradient descent on the parameters of an ANN, the network function (which maps input vectors to output vectors) follows the kernel gradient of the functional cost w.r.t. a new kernel: the NTK.” They also showed that when a finite layer version of the NTK is trained with gradient descent, its performance converges to the infinite-width limit NTK and then stays constant during training.
Some NeurIPS papers that build upon NTK:
- Learning and Generalization in Overparameterized Neural Networks, Going Beyond Two Layers
- On the Inductive Bias of Neural Tangent Kernels
However, many believe that NTK can’t fully explain deep learning. The hyperparameter settings needed for a neural net to approach the NTK regime – small learning rate, large initialization, no weight decay – aren’t often used to train neural networks in practice. The NTK perspective also states that neural networks would only generalize as well as kernel methods, but empirically they have been observed to generalize better.
Colin Wei et. al’s paper Regularization Matters: Generalization and Optimization of Neural Nets v.s. their Induced Kernel theoretically demonstrates that neural networks with weight decay can generalize much better than NTK, suggesting that studying L2-regularized neural networks could offer better insights into generalization. The following papers from this NeurIPS also show that conventional neural networks can outperform NTK:
- What Can ResNet Learn Efficiently, Going Beyond Kernels?
- Limitations of Lazy Training of Two-layers Neural Network
Many papers analyze the behavior of different components of neural networks. Chulhee Yun et al. presented Small ReLU networks are powerful memorizers: a tight analysis of memorization capacity and showed that “3-layer ReLU networks with Omega(sqrt(N)) hidden nodes can perfectly memorize most datasets with N points.”
Shirin Jalali et al.’s paper Efficient Deep Learning of Gaussian Mixture Models started with the question: “The universal approximation theorem states that any regular function can be approximated closely using a single hidden layer neural network. Can depth make it more efficient?” They showed that in the case of optimal Bayesian classification of Gaussian Mixture Models, such functions can be approximated with arbitrary precision using O(exp(n)) nodes in a neural network with one hidden layer, but only O(n) nodes in a two-layer network.
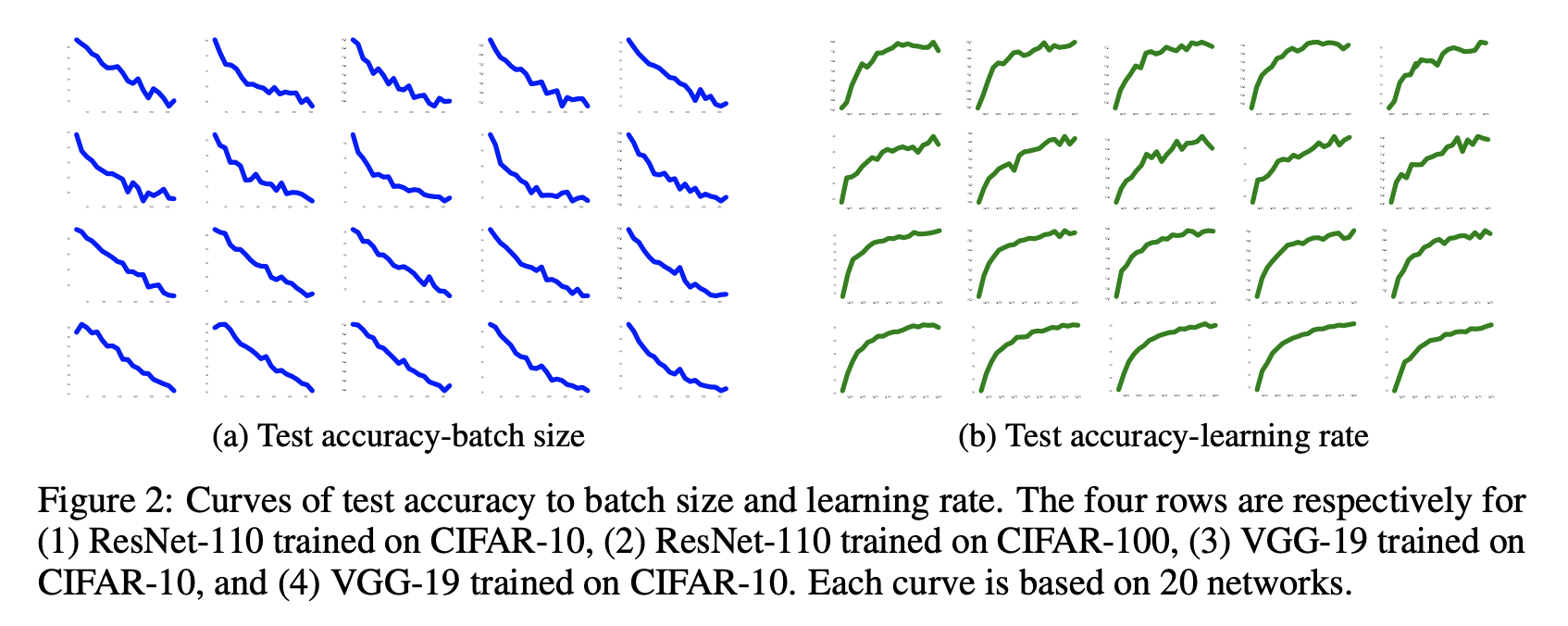
In one of the more practical papers, Control Batch Size and Learning Rate to Generalize Well: Theoretical and Empirical Evidence, Fengxiang He and team trained 1,600 ResNet-110 and VGG-19 models using SGD on CIFAR datasets and found that the generalization capacity of these models correlate negatively with batch size, positively with learning rate, and negatively with batch size/learning rate ratio.
At the same time, Yuanzhi Li et al.’s Towards Explaining the Regularization Effect of Initial Large Learning Rate in Training Neural Networks states that “a two layer network trained with large initial learning rate and annealing provably generalizes better than the same network trained with a small learning rate from the start … because the small learning rate model first memorizes low noise, hard-to-fit patterns, it generalizes worse on higher noise, easier-to-fit patterns than its large learning rate counterpart.”
While these theoretical analyses are fascinating and important, it can be hard to aggregate them into a big picture because each of them focuses on one narrow aspect of the system.
2. New approaches to deep learning
NeurIPS this year featured a wide range of methods outside stacking layers on top of each other. The three directions I’m excited about: Bayesian learning, graph neural networks, and convex optimization.
2.1 Deep learning with Bayesian principles
Bayesian learning and deep learning are very different, as highlighted by Emtiyaz Khan in his invited talk Deep Learning with Bayesian Principles. According to Khan, deep learning uses a ‘trial and error’ approach – let’s see where experiments take us – whereas Bayesian principles force you to think of a hypothesis (priors) beforehand.

Compared to regular deep learning, there are two main appeals to Bayesian deep learning: uncertainty estimation and better generalization on small datasets. In real world applications, it’s not enough that a system makes a prediction. It’s important to know how certain it’s about each prediction. For example, a prediction of cancer with 50.1% certainty requires different treatments from the same prediction with 99.9% certainty. With Bayesian learning, uncertainty estimation is a built-in feature.
Traditional neural networks give single point estimates – they output a prediction on a datapoint using a single set of weights. Bayesian neural networks, on the other hand, use a probability distribution over the network weights and output an average prediction of all sets of weights in that distribution, which has the same effect as averaging over many neural networks. Thus, Bayesian neural networks are natural ensembles, which act like regularization and can prevent overfitting.
Bayesian neural networks with millions of parameters are still computationally expensive to train. Converging to a posterior might take weeks, so approximating methods such as variational inference have become popular. The Probabilistic Methods – Variational Inference session features 10 papers on this variational Bayesian approach.
Some NeurIPS papers on Bayesian deep learning that I enjoyed reading:
- Importance Weighted Hierarchical Variational Inference
- A Simple Baseline for Bayesian Uncertainty in Deep Learning
- Practical Deep Learning with Bayesian Principles
2.2 Graph neural networks (GNNs)
For years, I’ve been talking about how graph theory is among the most underrated topics in machine learning. I’m glad to see graphs are all the rage at NeurIPS this year.
Graph representation learning is the most popular workshop of the day at #NeurIPS2019 . Amazing how far the field has advanced. I did not imagine so many people would get into this when I started working on graph neural nets back in 2015 during an internship. Time flies... pic.twitter.com/H8LM0BMvK4
— Yujia Li (@liyuajia) December 13, 2019
Graphs are beautiful and natural representations for many types of data such as social networks, knowledge bases, game states. The user-item data used for recommendation systems can be represented as a bipartite graph in which one disjoint set consists of users and another consists of items.
Graphs can also represent outputs of neural networks. As Yoshua Bengio reminded us in his invited talk, any joint distribution can be represented as a factor graph.
This makes graph neural networks perfect for tasks such as combinatorial optimization (e.g. travelling salesman, scheduling), identity matching (is this Twitter user the same as this Facebook user?), recommendation systems.
The most popular graph neural network is graph convolutional neural network (GCNN), which is expected since they both encode local information. Convolutions encode a bias towards finding relationships between neighboring parts of the inputs. Graphs encode the most closely related parts of the input via edges.
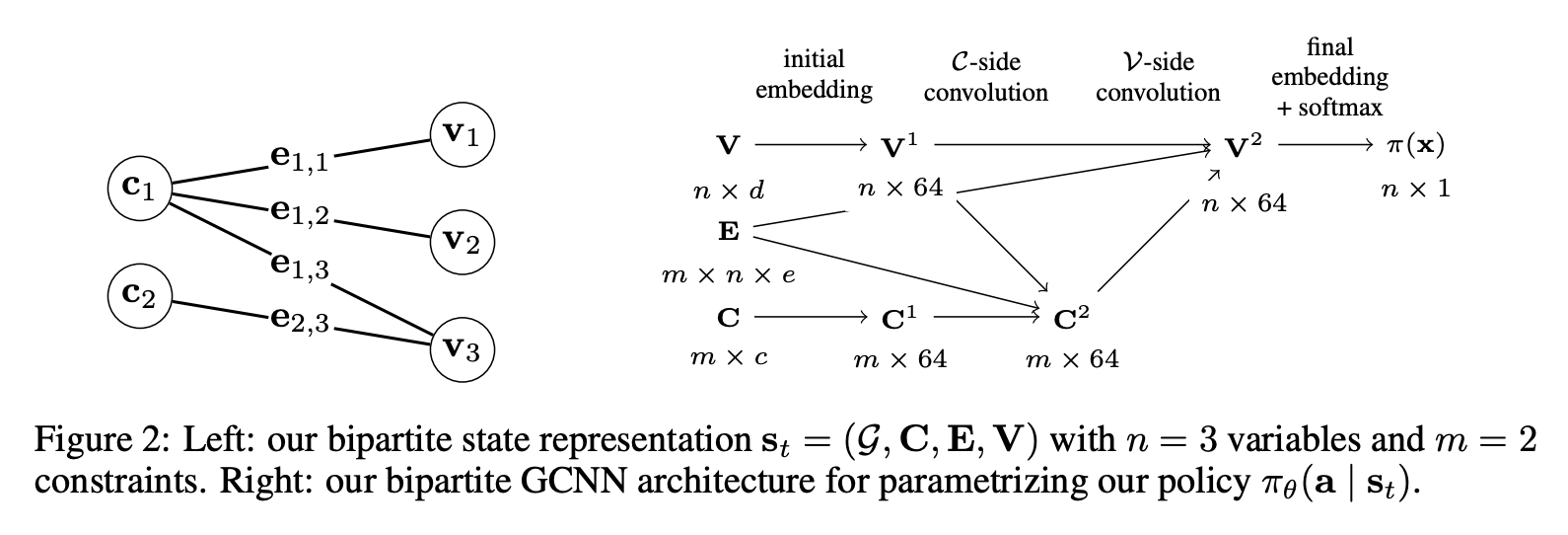
Some papers on GNNs that I like:
- Exact Combinatorial Optimization with Graph Convolutional Neural Networks
- Yes, there’s a paper that fuses two hottest trends this year: Graph Neural Tangent Kernel: Fusing Graph Neural Networks with Graph Kernels
- My favorite poster presentation at NeurIPS: (Nearly) Efficient Algorithms for the Graph Matching Problem on Correlated Random Graphs

Recommended reading outside NeurIPS:
- Thomas N. Kipf’s Graph Convolutional Networks blog post
- Kung-Hsiang, Huang’s A Gentle Introduction to Graph Neural Networks (Basics, DeepWalk, and GraphSage)
2.3 Convex optimization
I’ve low-key worshipped Stephen Boyd’s work on convex optimization from afar, so it was delightful to see it getting more popular at NeurIPS – there are 32 papers related to the topic (1, 2). Stephen Boyd and J. Zico Kolter’s labs also presented their paper Differentiable Convex Optimization Layers which showed how to differentiate through the solutions of convex optimization problems, making it possible to embed them in differentiable programs (e.g. neural networks) and learn them from data.
Convex optimization problems are appealing because they can be solved exactly (1e-10 error tolerance is attainable) and quickly. They also don’t produce weird/unexpected outputs, which is crucial for real-world applications. Even though many problems encountered in the wild are nonconvex, decomposing them into a sequence of convex problems can work well.
Neural networks are also trained using algorithms for convex optimization. However, while the emphasis in neural networks is to learn things from scratch, in an end-to-end fashion, applications of convex optimization problems emphasize modeling systems explicitly, using domain-specific knowledge. When it’s possible to model a system explicitly, in a convex way, usually much less data is needed. The work on differentiable convex optimization layers is one way to mix the benefits of end-to-end learning and explicit modeling.
Convex optimization is especially useful when you want to control a system’s outputs. For example, SpaceX uses convex optimization to land its rockets, and BlackRock uses it for trading algorithms. It’d be really cool to see convex optimization used in deep learning, the way Bayesian learning is now.
Some NeurIPS papers on convex optimization recommended by Akshay Agrawal.
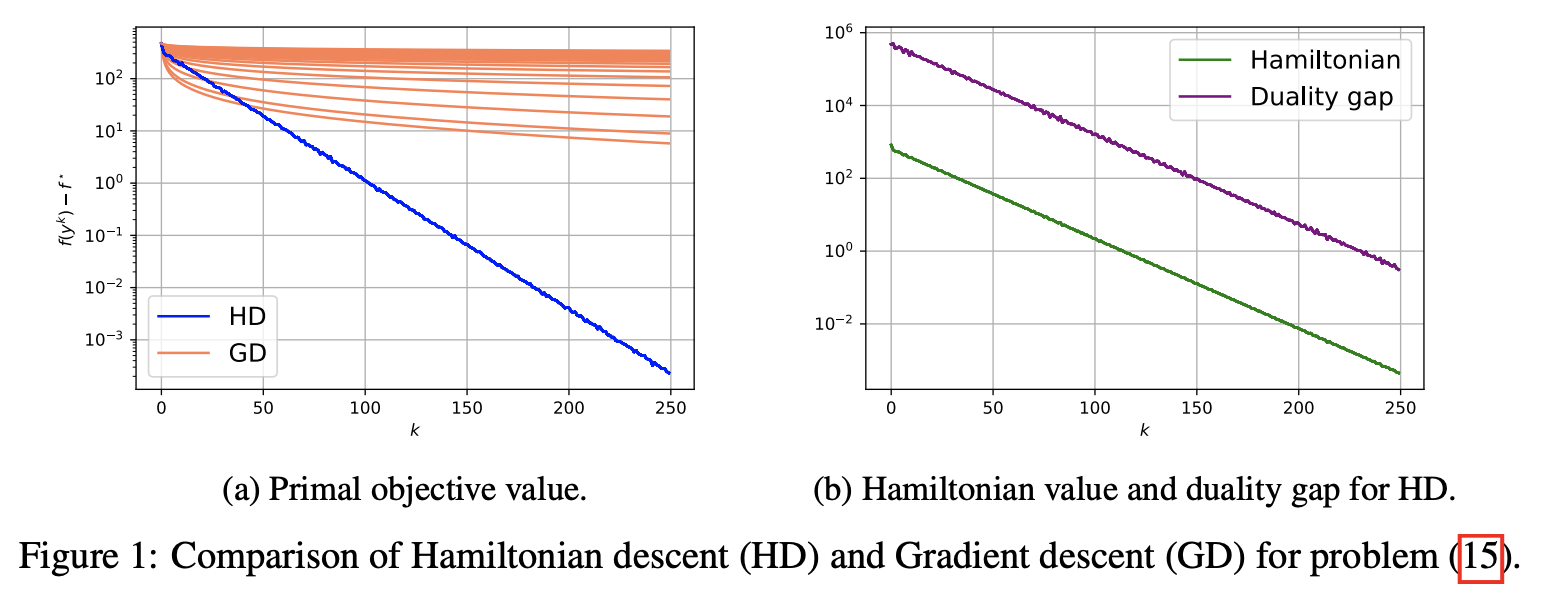
- Acceleration via Symplectic Discretization of High-Resolution Differential Equations
- Hamiltonian descent for composite objectives
3. Neuroscience x Machine Learning
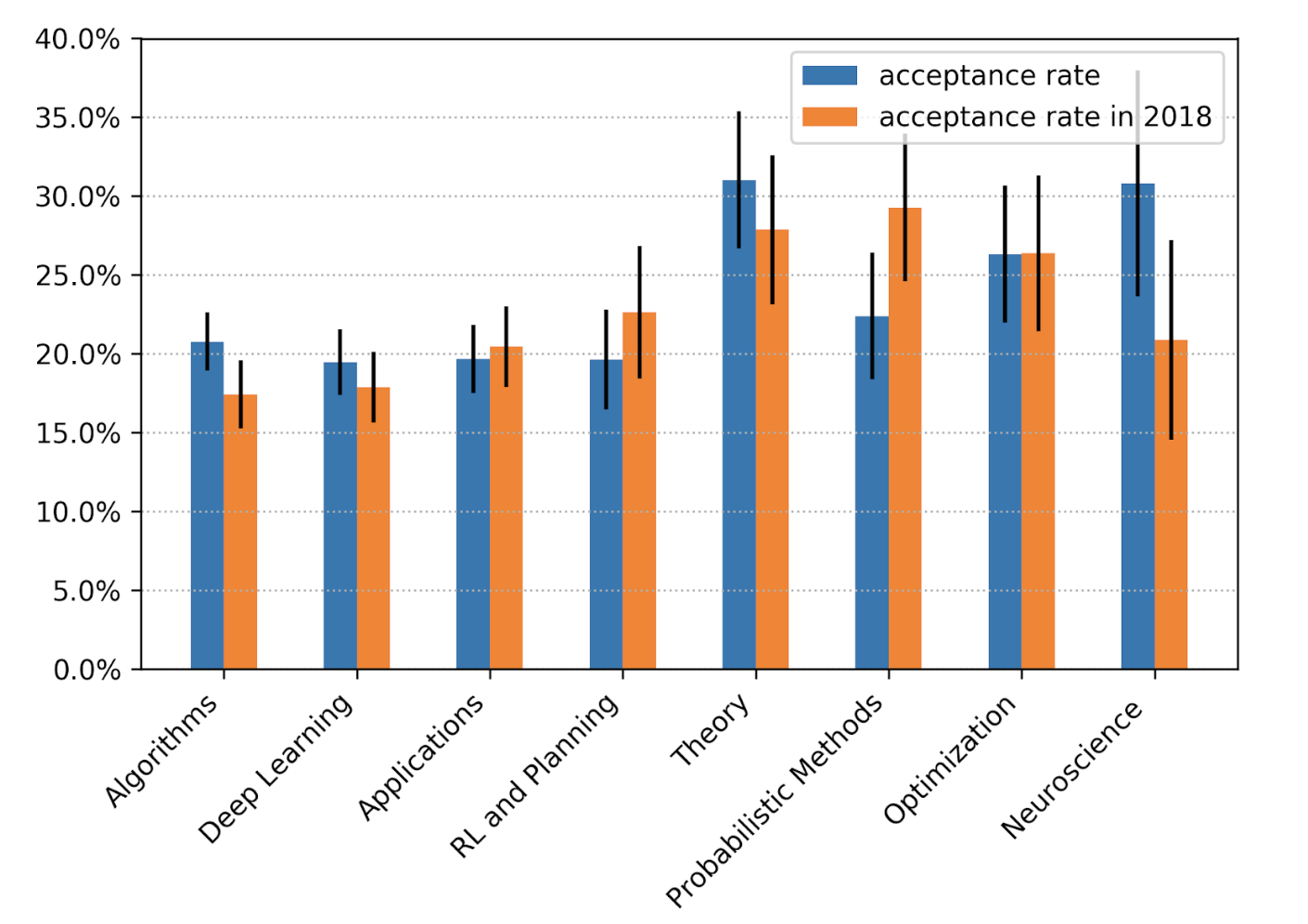
According to the analysis of NeurIPS 2019 Program Chair Hugo Larochelle, the category that got the highest pump in acceptance rate is Neuroscience. In their invited talks, both Yoshua Bengio (From System 1 Deep Learning to System 2 Deep Learning) and Blaise Aguera y Arcas (Social Intelligence) urged the machine learning community to think more about the biological roots of natural intelligence.
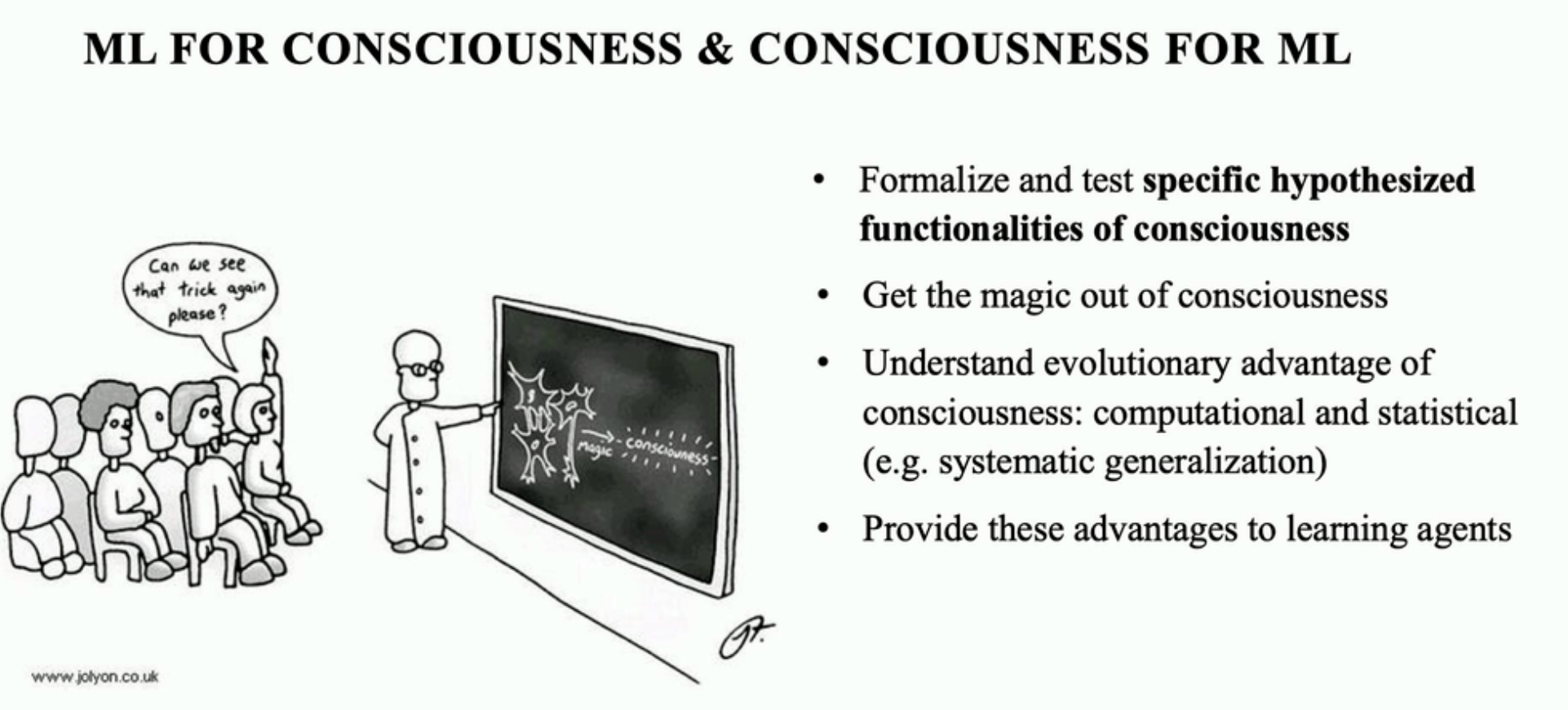
Bengio’s talk introduced consciousness into the mainstream machine learning vocabulary. The core ingredient of Bengio’s consciousness is attention. He compared machine attention mechanism to the way our brains choose what to pay attention to: “Machine learning can be used to help brain scientists better understand consciousness, but what we understand of consciousness can also help machine learning develop better capabilities.” According to Bengio, a consciousness-inspired approach is the way to go if we want machine learning algorithms that can generalize to out-of-distribution samples.
Aguera y Arcas’s talk is my favorite at the conference. It’s theoretically rigorous but practical. He argued how optimization is inadequate to capture human-like intelligence: “Optimization is not how life works… Brains don’t just evaluate a function. They develop. They’re self-modifying. They learn through experience. A function doesn’t have those things.” He called for “a more general, biologically inspired synapse update rule that allows but doesn’t require a loss function and gradient descent.”
This NeurIPS trend is consistent with my observation that many people in AI are moving to neuroscience. They bring neuroscience back into machine learning.
Some of the smartest people I know are leaving AI research for engineering/neuroscience. Their reasons?
— Chip Huyen (@chipro) November 15, 2019
1. We need to understand how humans learn to teach machines to learn.
2. Research should be hypothesis -> experiments, but AI research rn is experiments -> justifying results.
4. Keyword analysis
Let’s check out a more global view of what papers at the conference were about. I first visualized all the 1,011 paper titles from NeurIPS 2018 and 1,428 papers titles from NeurIPS 2019 with vennclouds. The black area in the middle is the list of words that are common in both 2018 and 2019 papers.

I then measured the proportional percentage change of these keywords from 2018 to 2019. For example, if in 2018, 1% of all the accepted papers have the keyword ‘X’ and in 2019, that number is 2%, then the proportional change is (2 - 1) / 1 = 100%. I plotted the keywords with the absolute proportional change of at least 20%.
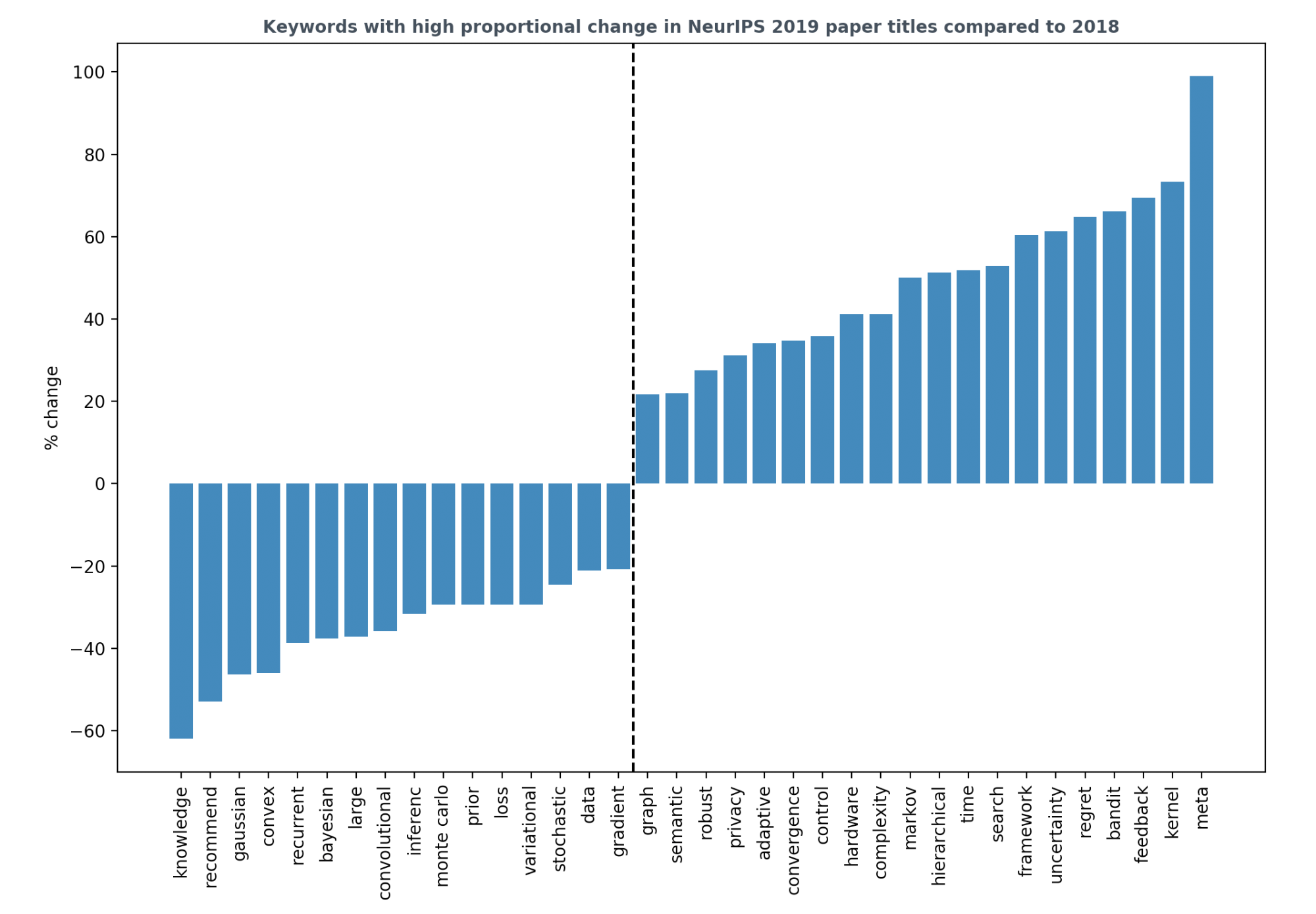
Key points:
- Reinforcement learning is gaining ground even outside robotics. Some of the keywords with significant positive change are bandit, feedback, regret, control.
- Generative models are still popular. GANs still capture our imagination, but are much less hype-y.
- Recurrent and convolutional neural networks are literally so last year.
- Hardware keyword is also on the rise, signaling more hardware-aware algorithms. This is the answer to the concern that hardware is the bottleneck in machine learning.
- I’m sad that data is on the decline. I was so excited to check out the Algorithms – Missing Data poster session only to find out it has one poster Missing Not at Random in Matrix Completion: The Effectiveness of Estimating Missingness Probabilities Under a Low Nuclear Norm Assumption.
- Meta sees the highest increase in proportion this year. Meta-meme by Jesse Mu.

- Even though Bayesian goes down, uncertainty goes up. Last year, there were many papers that use Bayesian principles, but not for deep learning.
5. NeurIPS by numbers
- 7k papers submitted to the main conference. 1,428 accepted papers. 21% acceptance rate.
- 13k attendees, which, by my estimation, means at least half of all attendees don’t present a paper there.
- 57 workshops, 4 focused on inclusion: Black in AI, Women in Machine Learning, LatinX in AI, Queer in AI, New In Machine Learning, Machine Learning Competitions for All.
- 16k pages of conference proceedings.
- 12% of all the accepted papers have at least one author from Google or Deepmind.
- 87 papers are from Stanford, making it the academic institution with the highest number of accepted papers.
Stuck at the airport so I browsed #neurips2019 papers.
— Chip Huyen (@chipro) September 7, 2019
Out of 1429 accepted papers, 167 (~12%) have at least one author from Google/DeepMind, same as Microsoft, Facebook, IBM, & Amazon combined.
Is there any stats on the % of reviewers who are Google/DeepMind affiliated? pic.twitter.com/bXPoB135PA
- 250 papers, 16.7%, are on applications.
- 648 is the number of citations as of Dec 2019 for the test of time award paper, Lin Xiao’s Dual Averaging Method for Regularized Stochastic Learning and Online Optimization. This is a proof that citation count and contribution don’t necessarily correlate.
- 75% of the papers with link to code in the camera-ready version, compared to only 50% from last year.
- 2,255 reviews mention looking at the code accompanying submission.
- 173 papers claimed for the Reproducibility Challenge on OpenReview.
- 31 posters at the NeurIPS Workshop on Machine Learning for Creativity and Design. Several people have told me it’s their favorite part of NeurIPS. Shout out to Good Kid the band for their amazing performance at the closing banquet. Check out their music on Spotify if you haven’t already!
Some days they are ML researchers, other days they are rockstars; tonight they are both! - Good Kid Band pic.twitter.com/Y8Y7eYrGkI
— Daniel Nkemelu (@DanielNkemelu) December 15, 2019
- 11 talks at the first Retrospectives: A Venue for Self-Reflection in ML Research workshop, which was another favorite.
The atmosphere of NeurIPS is captured well by atteendess on Twitter.
A fun little demonstration of the scale of #NeurIPS2019 - video of people heading into keynote talk.
— Andrey Kurenkov 🤖 @ Neurips (@andrey_kurenkov) December 12, 2019
This is 9 minutes condensed down to 15 seconds, and this is not even close to all the attendees! pic.twitter.com/1VqAHZoqtj
I went to NeurIPS for the first time in 2015. I believe it was in Montreal. I wrote about my terrible experience and was going to share anonymously but friends told me that it would be obvious who wrote it :) 4 years later, this conference has changed a lot 1\
— Timnit Gebru (@timnitGebru) December 15, 2019
Conclusion
I found NeurIPS overwhelming, both knowledge-wise and people-wise. I don’t think anyone can read 16k pages of the conference proceedings. The poster sessions are oversubscribed which makes it hard to talk to the authors. I undoubtedly missed out on a lot. If there’s a paper you think I should read, please let me know!
However, the massiveness of the conference also means a confluence of many research directions and people to talk to. It was nice to be exposed to work outside my subfield and learn from researchers whose backgrounds and interests are different from my own.
It was also great to see the research community moving away from the ‘bigger, better’ approach. My impression walking around the poster sessions is that many papers only experimented on small datasets such as MNIST and CIFAR. The best paper award, Ilias Diakonikolas et al.’s Distribution-Independent PAC Learning of Halfspaces with Massart Noise, doesn’t have any experiment.
I’ve often heard young researchers worrying over having to join big research labs to get access to computing resources, but NeurIPS proves that you can make important contributions without throwing data and compute at a problem.
During a NewInML panel that I was a part of, someone said he didn’t see how the majority of papers at NeurIPS could be used in production. Neil Lawrence said maybe he should look into other conferences. NeurIPS is more theoretical than many other machine learning conferences, and it’s okay. It’s important to pursue fundamental research.
Overall, I had a great time at NeurIPS, and am planning on attending it again next year. However, for those new in machine learning, I’d recommend ICLR as their first academic conference. It’s smaller, shorter, and more application-oriented. Next year, ICLR will be in Ethiopia, an amazing country to visit.
Acknowledgment
I’d like to thank Akshay Agrawal, Andrey Kurenkov, and Colin Wei for helping me with this draft. Fun fact: Colin Wei is one of a few PhD candidates with 4 papers accepted at NeurIPS this year – 3 of them made spotlight!