Predictive Human Preference: From Model Ranking to Model Routing

A challenge of building AI applications is choosing which model to use. What if we don’t have to? What if we can predict the best model for any prompt? Predictive human preference aims to predict which model users might prefer for a specific query.

Human preference has emerged to be both the Northstar and a powerful tool for AI model development. Human preference guides post-training techniques including RLHF and DPO. Human preference is also used to rank AI models, as used by LMSYS’s Chatbot Arena.

Chatbot Arena aims to determine which model is generally preferred. I wanted to see if it’s possible to predict which model is preferred for each query.

One use case of predictive human preference is model routing. For example, if we know in advance that for a prompt, users will prefer Claude Instant’s response over GPT-4, and Claude Instant is cheaper/faster than GPT-4, we can route this prompt to Claude Instant. Model routing has the potential to increase response quality while reducing costs and latency.

Another use case of predictive human preference is interpretability. Mapping out a model’s performance on different prompts can help us understand this model’s strengths and weaknesses. See section Experiment results for examples.

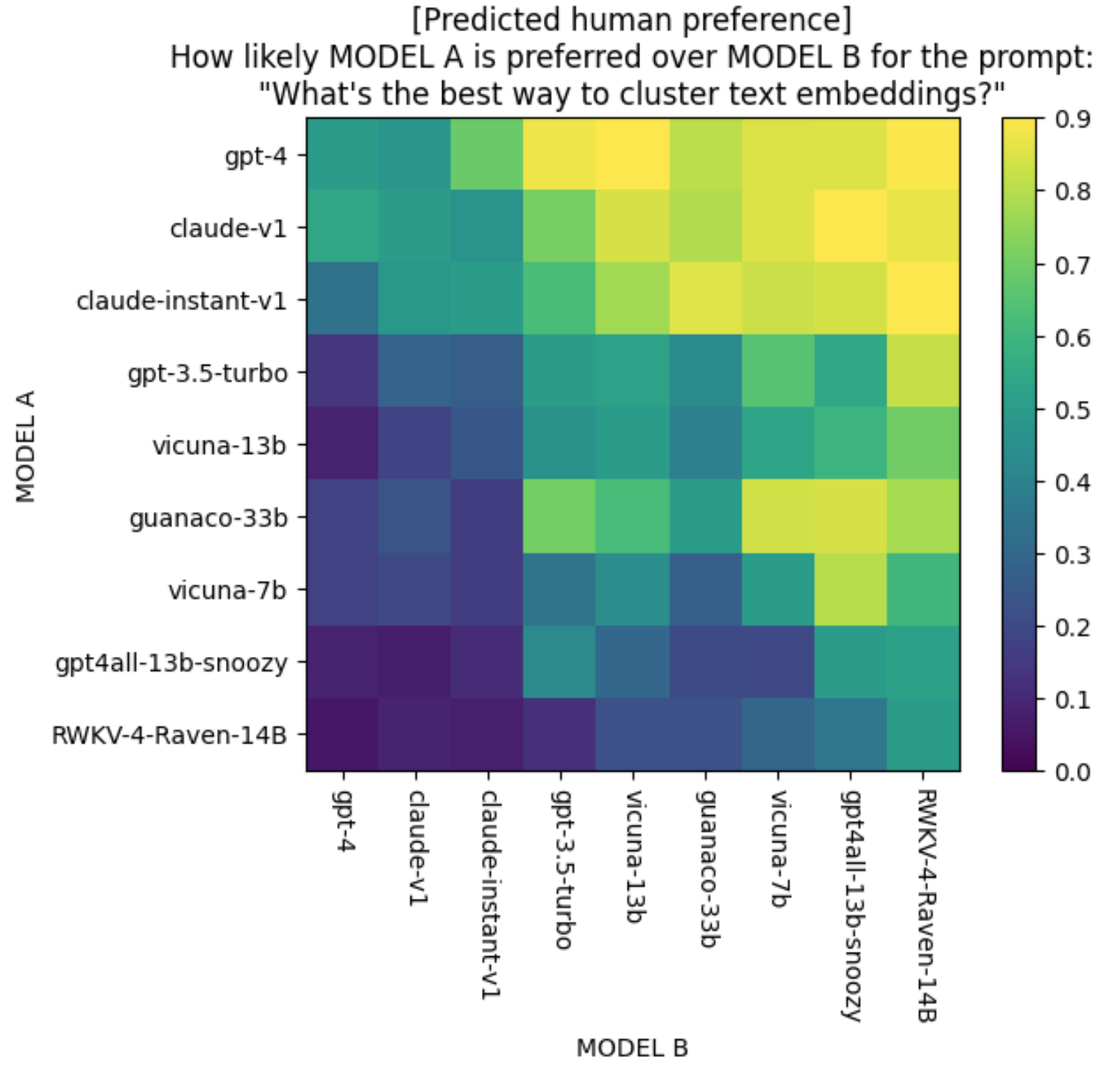
Here’s what predictive human preference for different model pairs looks like for the prompt “What’s the best way to cluster text embeddings?”. The predictions were generated by my toy preference predictor. The bright yellow color for the (GPT-4, GPT-3.5-Turbo) cell means that my predictor thinks GPT-4’s response is very likely to be preferred to that of GPT-3.5-Turbo’s for this prompt.

This post first discusses the correctness of Chatbot Arena, which will then be used as a baseline to evaluate the correctness of preference predictions. It then discusses how to build a preference predictor and the initial results.

Ranking Models Using Human Preference

Using preferential signals (comparisons) to rank models has grown in popularity in the last few years. Other than powering LMSYS’s Chatbot Arena, it’s also used by many model providers (Anthropic, Gemini, ChatGPT, etc.) to evaluate their models in production.

Side note: Friends who have deployed this in production told me that most users don’t read both options and just randomly vote for one. This introduces a lot of noise. However, the signals from the small percentage of users who vote correctly can sometimes be sufficient to help determine which model is preferred, as long as there’s minimal bias in the random voting.

How Preferential Ranking Works

Preferential ranking works in two steps:

1. Collect comparison data about user preference.
2. Compute a model ranking from these comparisons.

For each request, two or more models are selected to respond. An evaluator, which can be human or AI, picks the winner. The evaluator shouldn’t know which models are being judged. Each comparison is called a match. This process results in a series of comparisons.

Match ID	Prompt	Model A	Model B	Winner
1	…	Model 1	Model 2	Model 1
2	…	Model 3	Model 1	Model 1
3	…	Model 1	Model 4	Model 4
...	...	...	...	...

From these comparisons, we need to compute the rankings of all models. The two most common ranking algorithms are Elo (from chess) and TrueSkill (from video games).

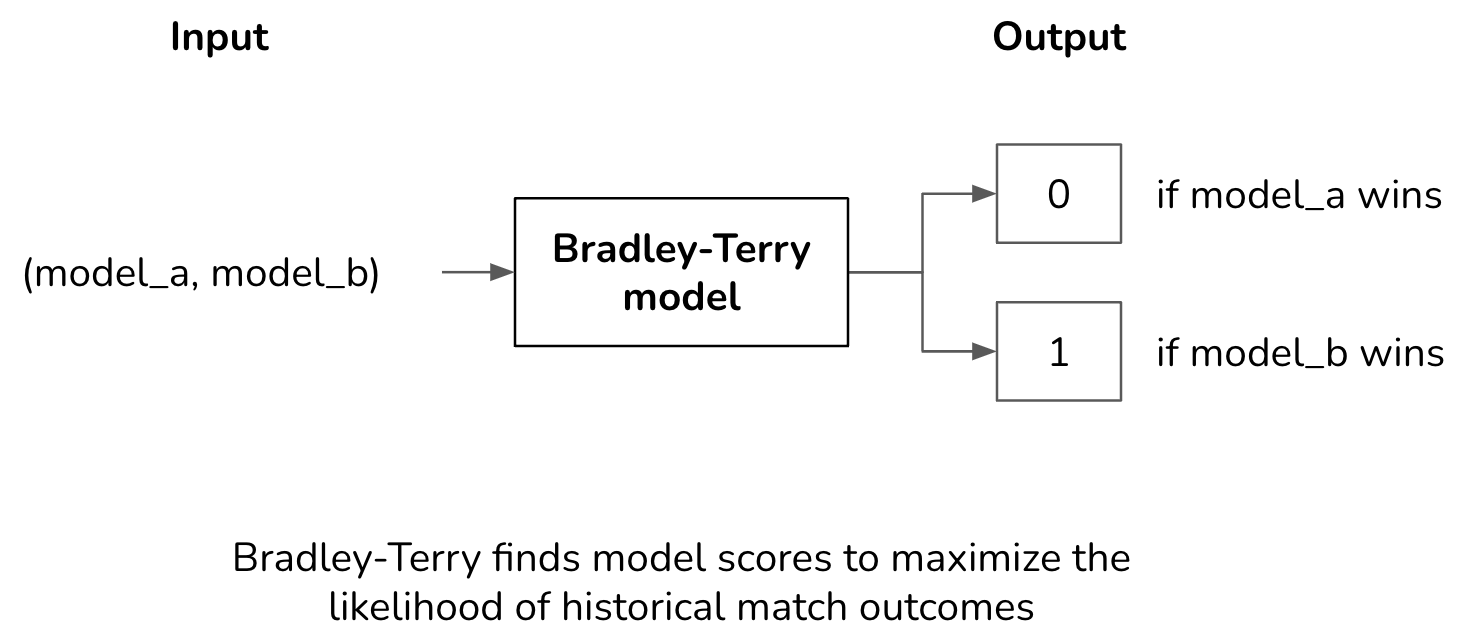
While Chatbot Arena refers to their model scores “Elo scores”, they actually don’t use Elo. In December 2023, they switched to Bradley-Terry but scaled the resulting scores to make them look Elo-like (see their notebook).

Given a history of match outcomes, the Bradley-Terry algorithm finds the model scores that maximize the likelihood of these match outcomes, turning model scoring into a maximum likelihood estimation problem. The input, for each training example, is the models that participate in the match. The output is the outcome of the match. Assuming there’s no draw, the outcome of a match is either 0 (a wins) or 1 (b wins).

Correctness of Chatbot Arena Ranking

Given the same match outcomes, different ranking algorithms can produce different rankings. For example, the ranking computed by Elo might differ from the ranking computed by Bradley-Terry. How do we know that a ranking is correct?

At its core, model ranking is a predictive problem. We compute a ranking from historical match outcomes and use it to predict future match outcomes. The quality of a ranking is determined by how accurately it can predict future match outcomes.

Let’s say we have a match between model A and model B. If model A has a higher score, meaning that the ranking algorithm predicts that A wins. If users indeed prefer the higher-ranking model, the ranking algorithm makes a correct prediction.

Eval data

To compute the accuracy of Chatbot Arena ranking, I used their data published in July 2023, which consists of 33K crowd-sourced comparisons for matches among 20 models. I used this smaller dataset instead of their Jan 2024 dataset because this smaller dataset contains the prompt used for each match, which I need for predictive human preference. Benchmarking on this dataset allows me to compare my model with the Bradley-Terry algorithm later on.

Here’s an example from their July 2023 dataset.

prompt	model_a	model_b	winner	model_a's response	model_b's response
who was the last monarch of uk	koala-13b	vicuna-13b	model_a	The last monarch of the United Kingdom was Queen Elizabeth II, who reigned from 1952 to 2020.	The current monarch of the United Kingdom is Queen Elizabeth II. She has been the monarch since 1952, and is the longest-reigning monarch in British history.

For reference, the Bradley-Terry (BT) scores of the top 7 models in this dataset are as follows.

1. GPT-4: 1189
2. Claude-v1: 1150
3. Claude-instant-v1: 1110
4. GPT-3.5-Turbo: 1104
5. WizardLM-13B: 1058
6. Vicuna-13b: 1040
7. Guanaco-33b: 1031

To create a test set, I randomly select 10% of the data (3300 examples). Each match has three possible outcomes: model_a wins, model_b wins, or tie. This can still be framed as a binary classification problem if we treat a tied match as two matches: one in which model_a wins and one in which model_b wins.

Results

I found that for all non-tie matches in my test set, the model with the higher Bradley-Terry score is preferred 74.1% of the time. This means that if we always predict the higher-ranked model as the winner for a match, we’d have an accuracy of 74.1%.

Test data	Output classes	# samples	BT's accuracy
All matches	model_a wins model_b wins tie	3,300	53.33%
Non-tie matches	model_a wins model_b wins	2,367	74.1%
Non-tie matches involving GPT-4	model_a wins model_b wins	355	85.1% (always pick GPT-4 as winner)

Back in July 2023, GPT-4 was considered the strongest model by a long shot (this was before Gemini, Mistral, Claude-v2). Did users always prefer GPT-4 to all other models? They didn’t. In 355 non-tie matches involving GPT-4, GPT-4 wins 85.1%.

This means that even though GPT-4 is the best model overall, there are prompts for which other models can outperform GPT-4. If we can figure out which prompts these are, and which models work best for them, we can route these prompts to the best-performing models, improving the response quality.

Predicting Human Preference For Each Prompt

If a ranking algorithm is about figuring out which model is better overall, predictive human preference is about figuring out which model is better for each prompt. If we know in advance that for a particular prompt, GPT-3.5 works just as well as GPT-4, and GPT-3.5 is cheaper, we can route that prompt to GPT-3.5 instead. Or if we know that Mistral-7B works just as well as GPT-4 and Mistral-7B is faster, we can route our query to Mistral-7B instead.

Model routing can also help with budget planning. Say, you only have enough budget to serve 50% of queries on the strongest model, and the rest to a weaker model, you want to make sure that you send to the weaker model only the queries that you’re confident it can do well on.

Experiment setup

I treat predictive human preference as a binary classification task. Given a match between 2 models, predict which one wins. If the probability of model_a winning is around 0.5, it can be considered a tie. If a Bradley-Terry model takes only (model_a, model_b) as the input, a preference predictor takes (prompt, model_a, model_b) as the input.

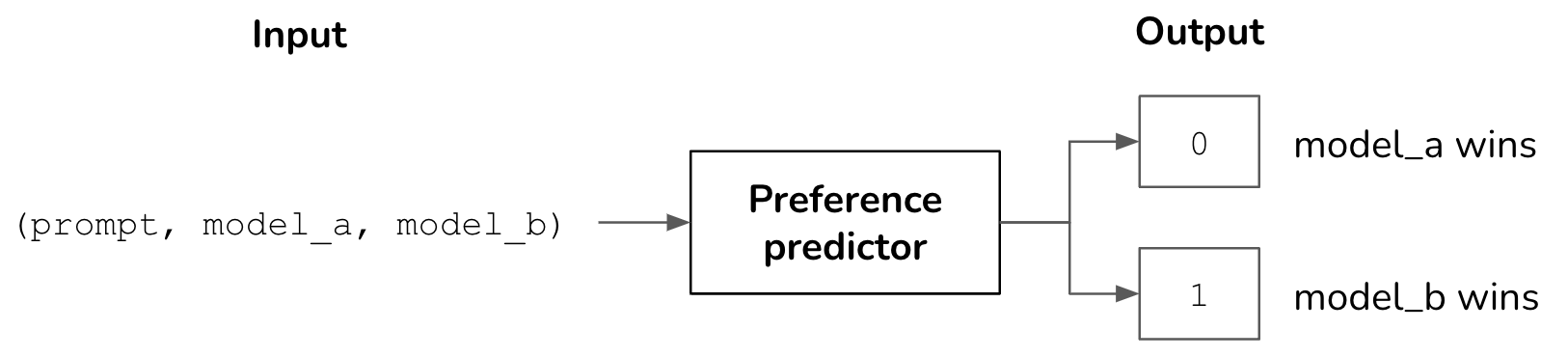
The architecture of my preference predictor looks like this. The model encoder and preference predictor are neural networks that can be trained independently or together. I used DistilBERT as my prompt encoder.

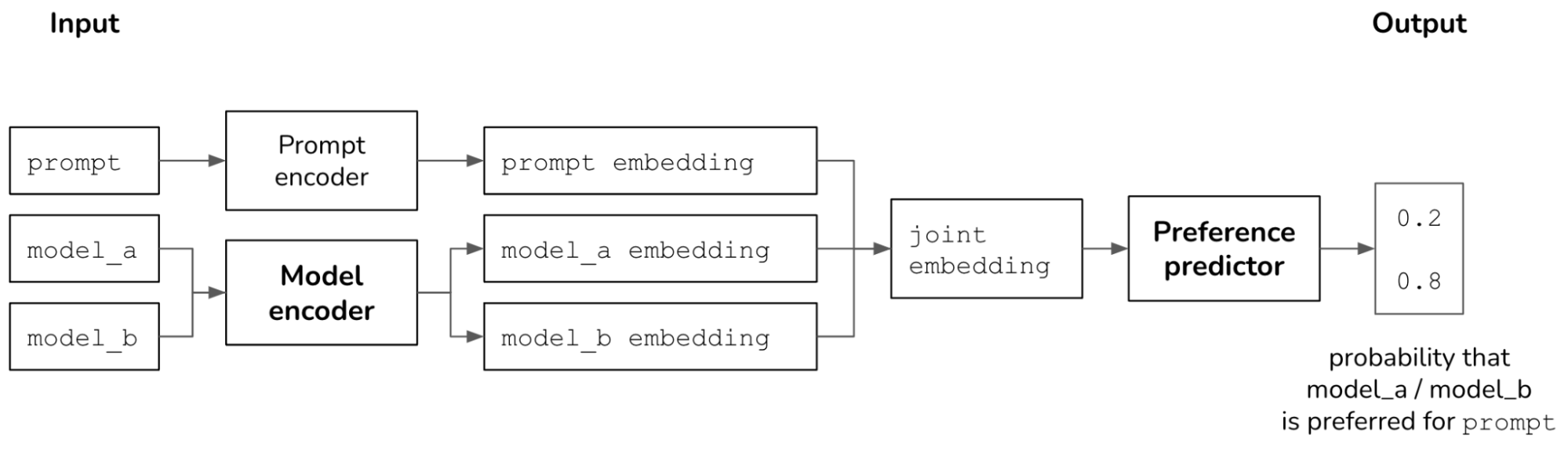
To train my model, I used 90% of LMSYS’s July 2023 dataset. I found that the predictor performed better using only non-tie matches (as opposed to using both tie and non-tie matches). I randomly flipped the order of models in a match 50% of the time.

To evaluate my model, I used 10% of this data. This is the same test data used to evaluate the correctness of Chatbot Arena’s ranking above.

Split	All matches	Non-tie matches
Train	29,700	20,927
Test	3,300	2,367

Note: I should’ve made a separate validation set for hyperparameter tuning. However, given that I didn’t have a lot of data and this is only a proof of concept, I didn’t do it. (I’m also lazy.) The matches are among 20 models, corresponding to 190 model pairs. 20,927 comparisons mean that, on average, there are only 110 comparisons per model pair.

Experiment results

I evaluated my preference predictor under two settings:

1. Using only model_a and model_b as the input. This is to see whether this predictor, using only model names, can make better predictions about match outcomes than Chatbot Arena scores.
2. Using (prompt, model_a, model_b) as the input. This is to see whether including prompts helps improve match outcome prediction.

I found that for all non-tie matches, my preference predictor can predict the match outcome accurately 75% of the time if not using prompts, and 76.2% of the time if using prompts. This suggests that human preference for models does change depending on the prompt. While the improvement doesn’t seem much, a 2.1% improvement can be significant at scale.

Eval data	# eval samples	Chatbot Arena	Preference predictor (without prompts)	Preference predictor (with prompts)
Non-tie matches	2,367	74.1%	75%	76.2%
Non-tie matches involving GPT-4	355	85.1%	86.2%	87%

Keep in mind that this predictor was trained with a small amount of crowd-sourced (e.g. noisy) data. The prompts crowdsourced are also simple. Among 33K prompts, 180 (0.55%) of them are “hello” and “hi”. These simple prompts are insufficient to distinguish strong models from weak ones. I suspect that with more/better data, the performance of this predictor can significantly improve.

Domain-specific and query-specific leaderboards

Recall that 20 models correspond to 190 model pairs. To visualize how the predictor captures human preference, for each evaluation prompt, I generated 190 different inputs, one for each model pair.

I then visualized the 190 predictions for 190 model pairs in a 20 x 20 grid, as shown below for the prompt “Derive the elastic wave equation.” I only included 9 models in the plot to make it readable. The diagonal values refer to comparing a model to itself, so the predicted preference should be 0.5.

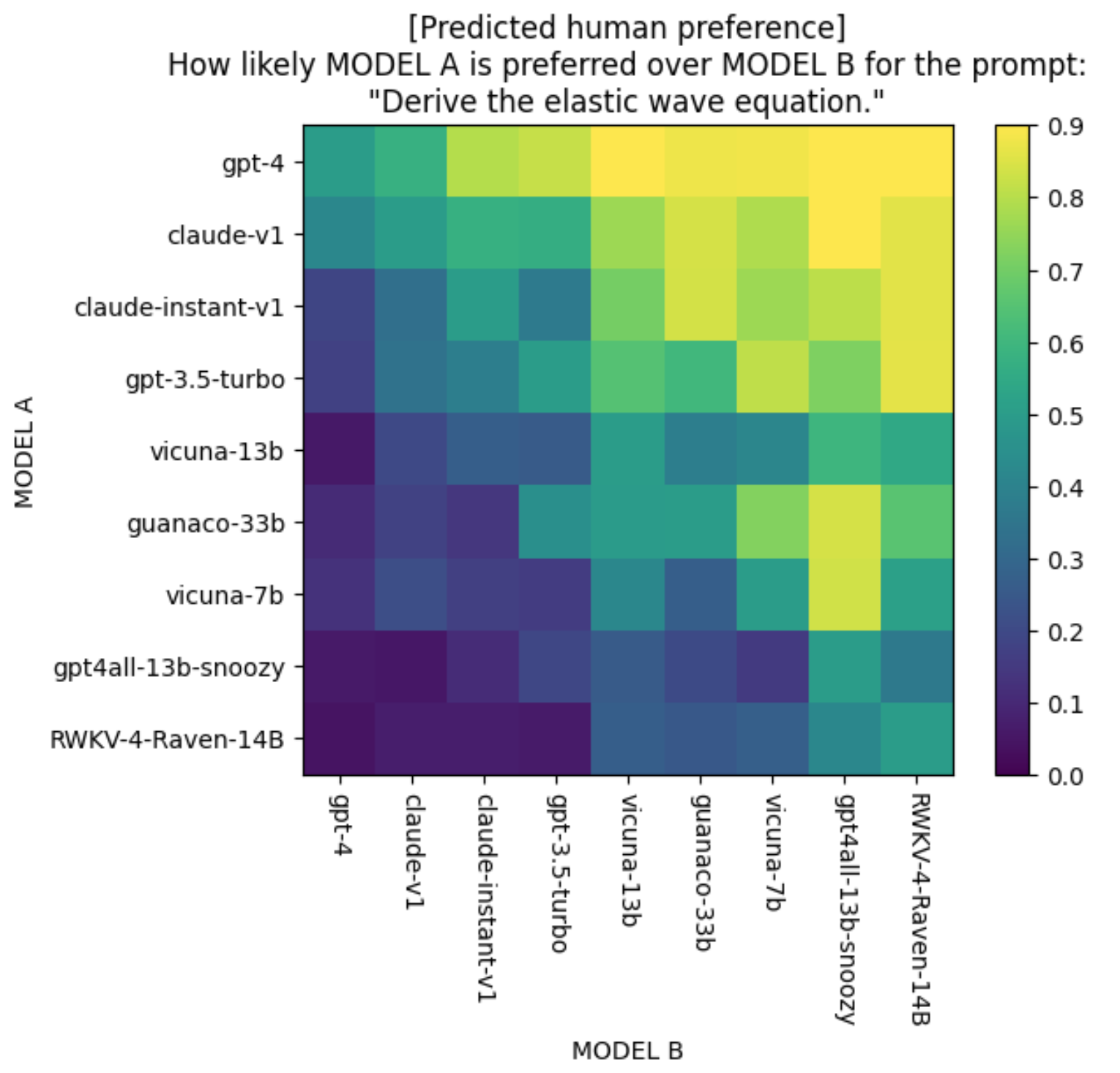
Given the predicted preference for all model pairs for a prompt, I used a Bradley-Terry model (the same ranking algorithm that LMSYS uses) to create a leaderboard for this prompt. I used the same scaling that LMSYS uses to make the scores look Elo-like. Here’s the ranking of the 9 models shown above for the query “Derive the elastic wave equation.”

This also means that with this preference predictor, we can create a leaderboard for any arbitrary subset of data. We can have a leaderboard specific to any domain.

Model ranking for the prompt"Derive the elastic wave equation."
gpt-4	1214
claude-v1	1162
gpt-3.5-turbo	1104
claude-instant-v1	1110
guanaco-33b	1023
vicuna-13b	1007
vicuna-7b	985
RWKV-4-Raven-14B	970
gpt4all-13b-snoozy	915

Despite being a toy predictor, the model seems to be able to capture different models’ performance patterns. One pattern is that for simple prompts, weak models can do (nearly) as well as strong models. For more challenging prompts, however, users are much more likely to prefer stronger models. Here’s a visualization of predicted human preference for an easy prompt (“hello, how are you?”) and a challenging prompt (“Explain why Planc length …”).

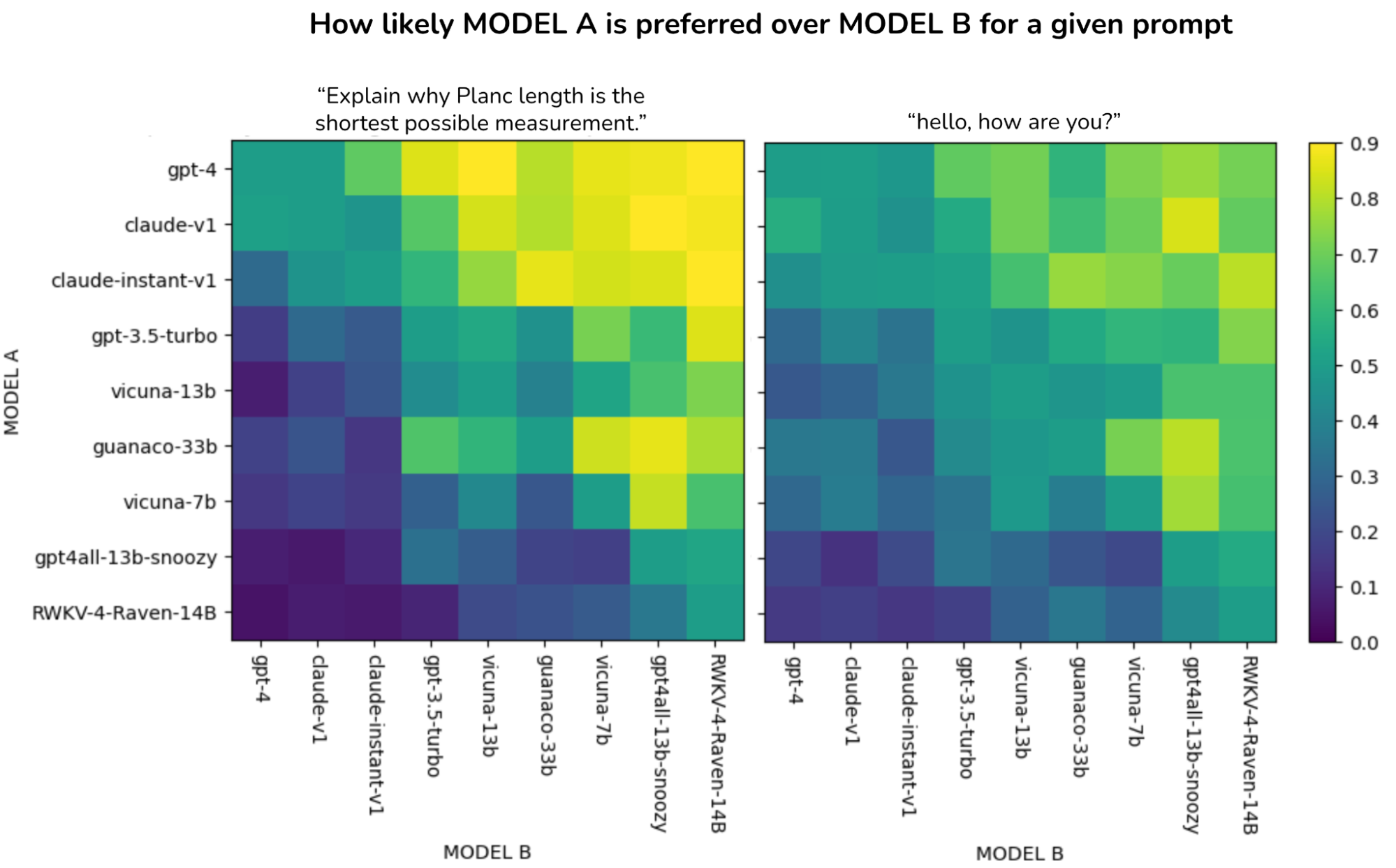
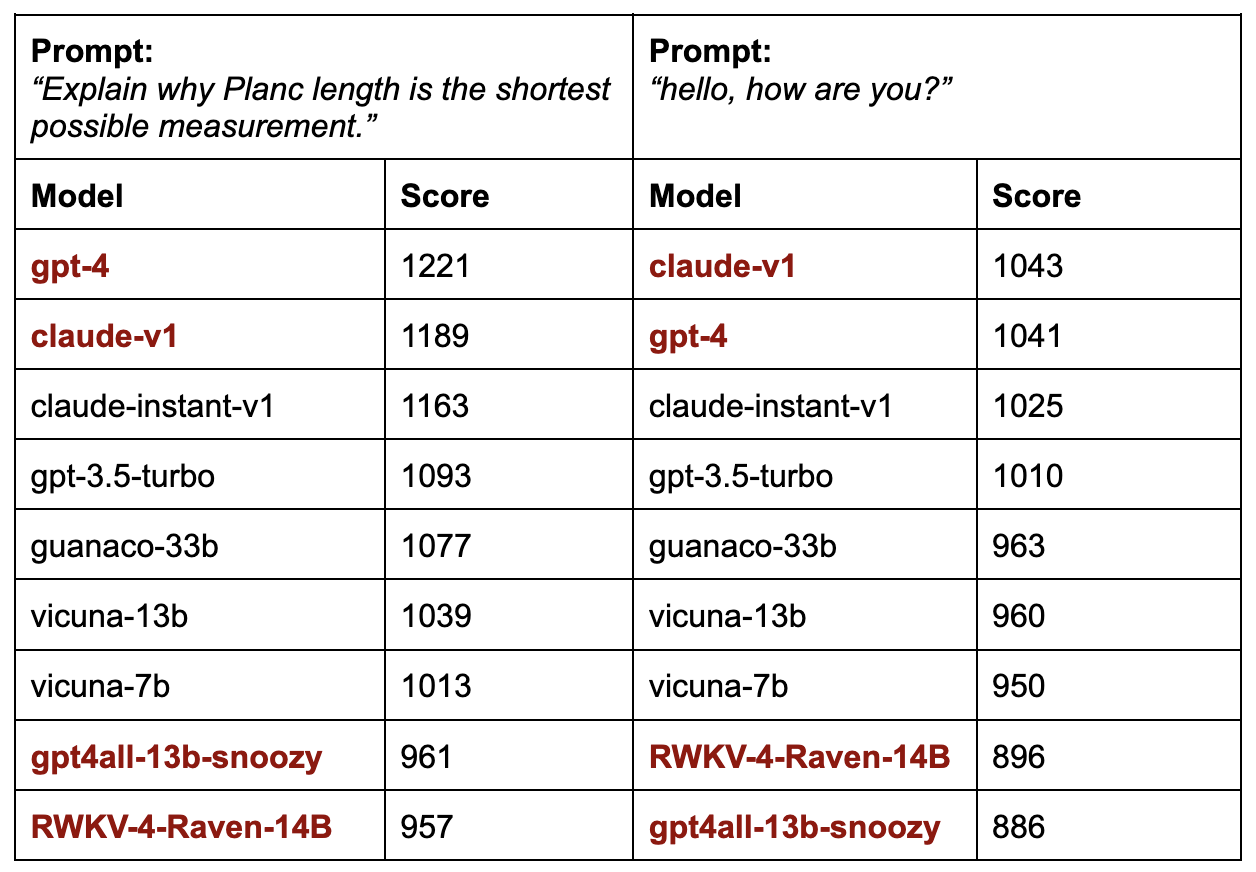
Here are the model rankings for these two prompts. The score spread for the simple prompt is much less than the score spread for the challenging prompt. The models that are ranked differently for these two prompts are highlighted in red.

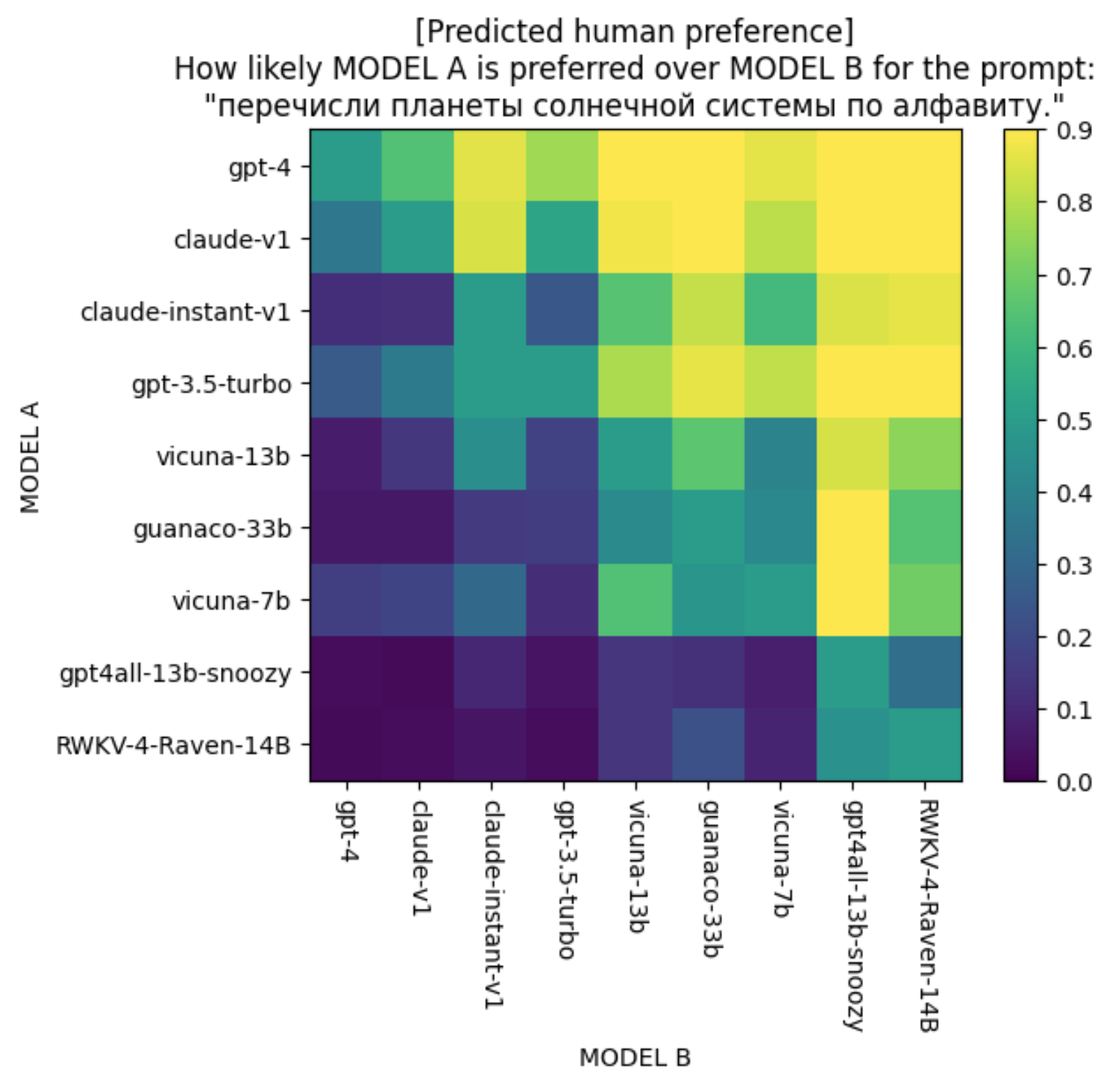
The predictor is also the most confident that GPT-4 will be preferred for queries in Russian and queries that involve code writing. For example, the average predicted win rate for the following Russian query of GPT-4 against all other models is 91.55%. Notice that for this query, while claude-v1 is predicted to do well on this query, claude-instant-v1 is predicted to do poorly.

Conclusion

My primitive experiment suggests that predictive human preference is feasible using a surprisingly small amount of data. There are many potential use cases for predictive human preference – model routing and interpretability are just two of them.

Predictive human reference is the first and the most important step in model routing (the other key step is routing strategy). With more and more models being developed, each with different capabilities and a cost structure, model routing has clear economic values.

I’m aware of four groups (two in stealth) that are working on model routing. One startup is Martian, which announced its $9M seed round. LMSYS is also working on model routing, which I think is a natural progression from their work in comparative evaluation.

While my experiment used human-annotated comparisons, LMSYS folks told me that due to the noisiness of crowd-sourced annotations and the costs of expert annotations, they’ve found that using GPT-4 to compare two responses works better. Depending on the complexity of the queries, generating 10,000 comparisons using GPT-4 would cost only $200 - 500, making this very affordable for companies that want to test it out.

This is the most fun side project I’ve worked on in a while, so I’d love to talk more about it. For those interested, I’ll be hosting a casual 30-minute discussion on predictive human preference on Tuesday, Mar 5, 9.30am PST. Join our Discord or email me if you want an invite!

Acknowledgment

Thanks Luke Metz for helping me with the experiments and coercing me into using JAX. While JAX is super cool and makes a lot of things easy, it also caused some of the weirdest bugs I’ve ever seen. I’m glad I used it though. Thanks Han-chung Lee for feedback on the plots.